How To Calculate Relative Rate Of Diffusion

Learning Objectives

By the end of this department, you volition be able to:

• Define and explain effusion and diffusion
• State Graham's law and use information technology to compute relevant gas properties

If you have ever been in a room when a piping hot pizza was delivered, you lot accept been made aware of the fact that gaseous molecules can quickly spread throughout a room, as evidenced by the pleasant smell that before long reaches your nose. Although gaseous molecules travel at tremendous speeds (hundreds of meters per second), they collide with other gaseous molecules and travel in many different directions before reaching the desired target. At room temperature, a gaseous molecule will experience billions of collisions per 2d. The hateful free path is the average altitude a molecule travels betwixt collisions. The mean costless path increases with decreasing pressure; in general, the mean free path for a gaseous molecule will be hundreds of times the bore of the molecule.

In general, we know that when a sample of gas is introduced to i office of a airtight container, its molecules very chop-chop disperse throughout the container; this process past which molecules disperse in space in response to differences in concentration is called diffusion (shown in Effigy 1). The gaseous atoms or molecules are, of course, unaware of any concentration gradient, they just move randomly—regions of higher concentration have more particles than regions of lower concentrations, and and then a net movement of species from high to low concentration areas takes place. In a closed environment, diffusion will ultimately result in equal concentrations of gas throughout, as depicted in Figure ane. The gaseous atoms and molecules continue to motility, merely since their concentrations are the same in both bulbs, the rates of transfer between the bulbs are equal (no internet transfer of molecules occurs).

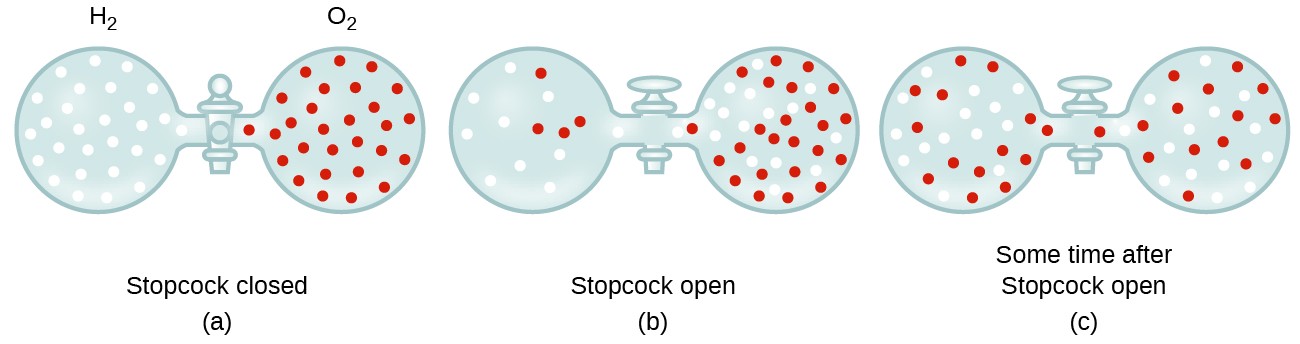
Figure 1. (a) Two gases, H₂ and O₂, are initially separated. (b) When the stopcock is opened, they mix together. The lighter gas, H_two, passes through the opening faster than O_two, so just after the stopcock is opened, more than H₂ molecules move to the O₂ side than O₂ molecules move to the H_ii side. (c) After a curt time, both the slower-moving O₂ molecules and the faster-moving H₂ molecules accept distributed themselves evenly on both sides of the vessel.

We are often interested in the rate of diffusion, the amount of gas passing through some area per unit time:

[latex]\text{rate of diffusion}=\frac{\text{amount of gas passing through an area}}{\text{unit of time}}[/latex]

The improvidence rate depends on several factors: the concentration slope (the increase or decrease in concentration from i indicate to another); the amount of surface area bachelor for diffusion; and the distance the gas particles must travel. Note also that the time required for diffusion to occur is inversely proportional to the rate of improvidence, every bit shown in the charge per unit of improvidence equation.

A process involving motility of gaseous species like to diffusion is effusion, the escape of gas molecules through a tiny hole such equally a pinhole in a balloon into a vacuum (Figure 2). Although diffusion and effusion rates both depend on the molar mass of the gas involved, their rates are non equal; all the same, the ratios of their rates are the aforementioned.

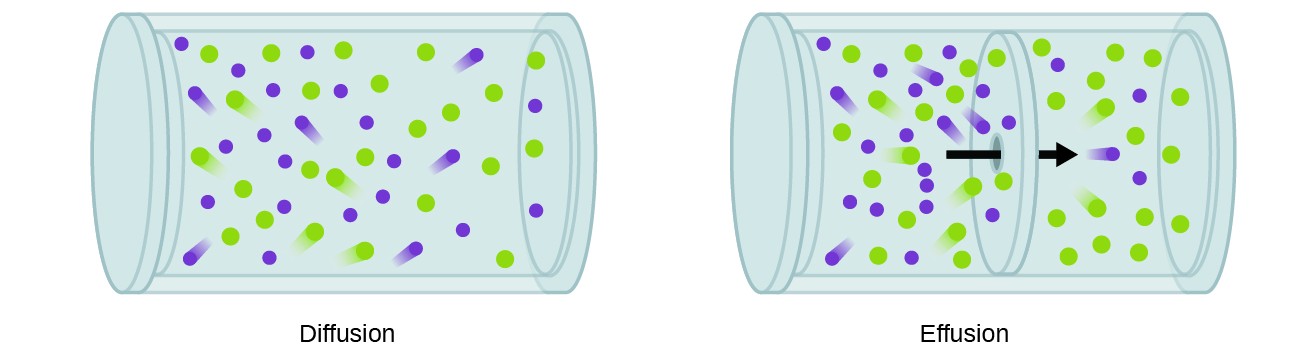
Figure 2. Diffusion occurs when gas molecules disperse throughout a container. Effusion occurs when a gas passes through an opening that is smaller than the mean complimentary path of the particles, that is, the average altitude traveled between collisions. Finer, this means that just one particle passes through at a time.

If a mixture of gases is placed in a container with porous walls, the gases effuse through the pocket-sized openings in the walls. The lighter gases pass through the pocket-size openings more than rapidly (at a higher rate) than the heavier ones (Effigy three). In 1832, Thomas Graham studied the rates of effusion of dissimilar gases and formulated Graham'due south police of effusion: The rate of effusion of a gas is inversely proportional to the square root of the mass of its particles:

[latex]\text{rate of effusion}\propto \frac{1}{\sqrt{\mathcal{M}}}[/latex]

This means that if 2 gases A and B are at the same temperature and pressure, the ratio of their effusion rates is inversely proportional to the ratio of the square roots of the masses of their particles:

[latex]\frac{\text{rate of effusion of A}}{\text{rate of effusion of B}}=\frac{\sqrt{{\mathcal{M}}_{\text{B}}}}{\sqrt{{\mathcal{One thousand}}_{\text{A}}}}[/latex]

Figure three. A balloon filled with air (the blueish one) remains full overnight. A airship filled with helium (the green 1) partially deflates because the smaller, light helium atoms effuse through pocket-size holes in the rubber much more readily than the heavier molecules of nitrogen and oxygen found in air. (credit: modification of piece of work by Mark Ott)

Example 1: Applying Graham's Law to Rates of Effusion

Calculate the ratio of the rate of effusion of hydrogen to the rate of effusion of oxygen.

Cheque Your Learning

At a particular pressure and temperature, nitrogen gas effuses at the rate of 79 mL/due south. Using the same apparatus at the aforementioned temperature and pressure level, at what rate volition sulfur dioxide effuse?

Here's another example, making the point nearly how determining times differs from determining rates.

Example 2: Effusion Fourth dimension Calculations

Information technology takes 243 s for 4.46 × 10^-v mol Xe to effuse through a tiny hole. Under the aforementioned conditions, how long will it take 4.46 × x^–5 mol Ne to effuse?

Check Your Learning

A party balloon filled with helium deflates to [latex]\frac{2}{3}[/latex] of its original book in 8.0 hours. How long will it take an identical balloon filled with the aforementioned number of moles of air (ℳ = 28.2 grand/mol) to deflate to [latex]\frac{1}{2}[/latex] of its original book?

Finally, here is i more example showing how to summate tooth mass from effusion charge per unit data.

Instance iii: Determining Molar Mass Using Graham's Law

An unknown gas effuses one.66 times more than chop-chop than CO_two. What is the molar mass of the unknown gas? Can you brand a reasonable guess every bit to its identity?

Check Your Learning

Hydrogen gas effuses through a porous container 8.97-times faster than an unknown gas. Estimate the molar mass of the unknown gas.

Use of Improvidence for Nuclear Energy Applications: Uranium Enrichment

Gaseous diffusion has been used to produce enriched uranium for utilise in nuclear ability plants and weapons. Naturally occurring uranium contains but 0.72% of ²³⁵U, the kind of uranium that is "fissile," that is, capable of sustaining a nuclear fission concatenation reaction. Nuclear reactors require fuel that is ii–5% ²³⁵U, and nuclear bombs need even college concentrations. One way to enrich uranium to the desired levels is to take advantage of Graham's police. In a gaseous improvidence enrichment institute, uranium hexafluoride (UF_vi, the only uranium compound that is volatile plenty to work) is slowly pumped through big cylindrical vessels called diffusers, which contain porous barriers with microscopic openings. The process is one of diffusion because the other side of the bulwark is not evacuated. The [latex]^{235}{\text{UF}}_{6}[/latex] molecules have a higher boilerplate speed and diffuse through the bulwark a little faster than the heavier [latex]^{238}{\text{UF}}_{six}[/latex] molecules. The gas that has passed through the bulwark is slightly enriched in [latex]^{235}{\text{UF}}_{half-dozen}[/latex] and the residual gas is slightly depleted. The small-scale difference in molecular weights between [latex]^{235}{\text{UF}}_{six}[/latex] and [latex]^{238}{\text{UF}}_{6}[/latex] just virtually 0.4% enrichment, is achieved in ane diffuser (Figure 4). But by connecting many diffusers in a sequence of stages (chosen a cascade), the desired level of enrichment can be attained.

The large scale separation of gaseous [latex]^{235}{\text{UF}}_{6}[/latex] from [latex]^{238}{\text{UF}}_{half dozen}[/latex] was offset done during the World War II, at the atomic energy installation in Oak Ridge, Tennessee, every bit part of the Manhattan Project (the development of the outset atomic bomb). Although the theory is simple, this required surmounting many daunting technical challenges to brand it work in practise. The barrier must take tiny, compatible holes (about 10^–6 cm in bore) and exist porous plenty to produce high period rates. All materials (the bulwark, tubing, surface coatings, lubricants, and gaskets) need to be able to contain, simply not react with, the highly reactive and corrosive UF₆.

Because gaseous diffusion plants require very big amounts of energy (to compress the gas to the loftier pressures required and drive it through the diffuser pour, to remove the oestrus produced during pinch, so on), it is now being replaced by gas centrifuge applied science, which requires far less energy. A current hot political upshot is how to deny this technology to Islamic republic of iran, to prevent it from producing plenty enriched uranium for them to utilise to make nuclear weapons.

Key Concepts and Summary

Gaseous atoms and molecules move freely and randomly through space. Improvidence is the procedure whereby gaseous atoms and molecules are transferred from regions of relatively high concentration to regions of relatively low concentration. Effusion is a similar process in which gaseous species pass from a container to a vacuum through very pocket-sized orifices. The rates of effusion of gases are inversely proportional to the square roots of their densities or to the square roots of their atoms/molecules' masses (Graham'south constabulary).

Key Equations

• [latex]\text{rate of diffusion}=\frac{\text{amount of gas passing through an area}}{\text{unit of time}}[/latex]
• [latex]\frac{\text{rate of effusion of gas A}}{\text{rate of effusion of gas B}}=\frac{\sqrt{{one thousand}_{B}}}{\sqrt{{m}_{A}}}=\frac{\sqrt{{\mathcal{Yard}}_{B}}}{\sqrt{{\mathcal{M}}_{A}}}[/latex]

Exercises

1. A balloon filled with helium gas is found to take 6 hours to deflate to 50% of its original volume. How long will it have for an identical balloon filled with the same book of hydrogen gas (instead of helium) to subtract its volume past 50%?
2. Explicate why the numbers of molecules are not identical in the left- and correct-hand bulbs shown in the center illustration of Figure 1.
3. Starting with the definition of rate of effusion and Graham'due south finding relating rate and molar mass, show how to derive the Graham's constabulary equation, relating the relative rates of effusion for two gases to their molecular masses.
4. Heavy h2o, D₂O (tooth mass = 20.03 g mol^–1), can be separated from ordinary water, H₂O (molar mass = 18.01), as a result of the deviation in the relative rates of diffusion of the molecules in the gas phase. Calculate the relative rates of improvidence of H₂O and D₂O.
5. Which of the following gases lengthened more slowly than oxygen? F₂, Ne, N_twoO, C_twoH_ii, NO, Cl₂, H_iiS
6. During the give-and-take of gaseous diffusion for enriching uranium, it was claimed that [latex]^{235}{\text{UF}}_{vi}[/latex] diffuses 0.four% faster than [latex]^{238}{\text{UF}}_{6}.[/latex] Show the adding that supports this value. The tooth mass of [latex]^{235}{\text{UF}}_{6}.[/latex] = 235.043930 + six × 18.998403 = 349.034348 g/mol, and the tooth mass of [latex]^{238}{\text{UF}}_{half dozen}.[/latex] = 238.050788 + half dozen × xviii.998403 = 352.041206 chiliad/mol.
7. Calculate the relative charge per unit of improvidence of [latex]^{one}{\text{H}}_{two}[/latex] (molar mass 2.0 g/mol) compared to that of [latex]^{2}{\text{H}}_{2}[/latex] (molar mass 4.0 g/mol) and the relative charge per unit of improvidence of O_ii (tooth mass 32 g/mol) compared to that of O_iii (molar mass 48 g/mol).
8. A gas of unknown identity diffuses at a charge per unit of 83.3 mL/s in a diffusion apparatus in which carbon dioxide diffuses at the charge per unit of 102 mL/s. Calculate the molecular mass of the unknown gas.
9. When two cotton plugs, one moistened with ammonia and the other with hydrochloric acid, are simultaneously inserted into opposite ends of a glass tube that is 87.0 cm long, a white band of NH₄Cl forms where gaseous NH₃ and gaseous HCl commencement come into contact. (Hint: Calculate the rates of diffusion for both NH₃ and HCl, and discover out how much faster NH_three diffuses than HCl.) [latex]{\text{NH}}_{3}\left(m\right)+\text{HCl}\left(grand\right)\rightarrow{\text{NH}}_{four}\text{Cl}\left(s\right)[/latex] At approximately what altitude from the ammonia moistened plug does this occur?

Glossary

improvidence:movement of an atom or molecule from a region of relatively loftier concentration to i of relatively low concentration (discussed in this chapter with regard to gaseous species, but applicable to species in whatsoever stage)

effusion:transfer of gaseous atoms or molecules from a container to a vacuum through very small-scale openings

Graham'south law of effusion:rates of diffusion and effusion of gases are inversely proportional to the square roots of their molecular masses

mean complimentary path:average distance a molecule travels between collisions
charge per unit of improvidence:amount of gas diffusing through a given area over a given fourth dimension

Source: https://courses.lumenlearning.com/suny-mcc-chemistryformajors-1/chapter/effusion-and-diffusion-of-gases/

Share this post